|
Klasikinės neišsprendžiamos geometrinės konstrukcijos Tai klasikiniai graikų geometrijos uždaviniai, kuriuos reikia išspręsti tenaudojant nesužymėtą liniuotę ir skriestuvą. Graikų dėmesys brėžimo uždaviniams, naudojant tik liniuotę ir skriestuvą, atitinka jų filosofinę nuostatą apie pasaulio įvairovės aiškinimą nurodant struktūrinius elementarius pagrindus. Paskutinių dviejų (pagal šiame straipsnelyje pateikiamą tvarką) negalimumą 1837 m. įrodė P. Vancelis1) (Liouville Journal), nors apie tai apie 1800-uosius žinojo ir K. Gausas. Kampo trisekcijos neišsprendžiamumą 1882 m. įrodė Lindemannas2). Įrodymai remiasi faktu, kad skaičiai, gauti naudojant tik nežymėtą liniuotę ir skriestuvą, išvedami iš duotų pradinių skaičių tik aritmetinių veiksmų (sudėties, atimties, daugybos ir dalybos) ir kvadratinės šaknies būdu. Tai vadinamieji Euklido skaičiai. Juos galima įsivaizduoti kaip skaičius, gaunamus pakartotinai sprendžiant kvadratines lygtis. Visiems tiems trim uždaviniams reikia arba traukti kubinę šaknį arba naudoti p. Kubinė šaknis nėra Euklido skaičiumi,
o Lindermanas įrodė, kad
p yra transcendentinis skaičius,
t.y. jis negali būti jokios algebrinės lygties su sveikaisiais koeficientais sprendiniu -
t.y., jis taipogi nėra Euklido skaičiumi. 1. Skritulio kvadratūra Duoto spindulio skrituliui nubrėžti tokio pat ploto kvadratą.
Daugelį traukė ši paprasta ir suprantama formuluotė, natūraliai sukelianti iliuziją, kad uždavinys lengvai išsprendžiamas. Ir kas senovėje galėjo pagalvoti, kad jo bus ieškoma net 2500 m. Jis pasirodė kietu riešutėliu ir mokslininkams, ir gausiems geometrijos mėgėjams. Visi sunkumai, su kuriais buvo susiduriama, tik didino uždavinio populiarumą. Prie jo prisidėjo ir kvadratintojų garbės troškimas, noras įeiti į istoriją arba bent gauti užtarnautą apdovanojimą. Bet koks susidomėjimo juo protrūkis sukeldavo skritulio kvadratūros epidemiją. Jiedu turi bendrą plotą tik tuo atveju, jei spindulio ir kvadrato kraštinės santykis lygus kvadratinei šakniai iš
p. Plačiau apie uždavinio istoriją skaitykite Išmatuojame apskritimą 2. Kubo padvigubinimas Duotai kubo kraštinei nubrėžti dvigubai didesnio tūrio kubą.
Dar vadinamas Deliano uždaviniu. Reikia surasti tokį kubo briaunos ilgį, kad jo tūris padvigubėtų. Šių
dienų terminais būtų - išspręsti x3 = 2 lygtį. Iš tikro, sprendžiant geometriniais metodais
naudojant tik liniuotę ir skriestuvą, jos išspręsti negalima, nes Deliano konstanta
Menaechmas ją išsprendė suradęs dviejų parabolių x 2 = y ir y 2 = 2x susikirtimą. Ją taip pat galima išspręsti naudojant neusis (ribojančią) konstrukciją, kai leidžiama slysti sužymėtai liniuotei. Ji leidžia išspręsti ir kampo trisekcijos ir taisyklingo heptagono sudarymo uždavinius. 1837 m. Pierre Wantzelis įrodė, kad šis uždavinys (kaip ir kampo trisekcijos) neišsprendžiamas naudojant tik tiesias linijas ir apskritimus (įrodymas išspausdintas Journal of Liouville) 3. Kampo trisekcija Duotam bet kokiam kampui nubrėžti kampą, lygų trečdaliui pradinio kampo.
Uždavinys ekvivalentiškas kubinės lygties sprendimui. Sprendžiama, kaip kampą padalinti į tris lygias dalis. Uždavinys iškilo, kai geometrai išmoko brėžti penkiakampį. Einant tolyn pasirodė, kad norint brėžti kitus n-kampius (ir kurių kraštinių skaičius kartotinis 9), reikia mokėti į tris dalis padalyti kampą. Uždavinys neišsprendžiamas plokštumos priemonėmis. Tarkime, kampas yra 60o. Tada: Kai a = 20o: Pakeitus x = cos a, gausime: v3 - 3v - 1 = 0 (*) Beliko parodyti, kad ši lygtis neturi racionaliųjų šaknų. Tarkim ji turi sprendinį p/q, kuris yra nesupaprastinama trupmena. Tada: Ją perrašykime: Iš čia, p turi dalyti q3, taigi ir q, t.y. (p | q). Iš kitos pusės, lygtį galime perrašyti taip: iš čia analogiškai seka, kad q dalija p, t.y. ( q | p ). O taip gali būti tik tada, kai p/q yra 1 arba -1, bet nė vienas šių atvejų netenkina (*) lygties. Plačiau apie Kampo trisekciją skaitykite Kampo trisekcija 1)
Pieras Vancelis (Pierre Laurent Wantzel, 1814-1848) prancūzų matematikas. nuo 1838 m. keliose
Paryžiaus mokymo įstaigose dėstė taikomąją mechaniką. Garsi jo 1837 m. publikacija, įrodanti klasikinių graikų
kubo padvigubinimo ir kampo trisekcijos uždavinių neišsprendžiamumą. Taip pat įrodė, kad skriestuvo ir liniuotės
pagalba neįmanoma nubrėžti taisyklinkų daugiakampių, kurių kraštų kiekis tenkina Gauso sąlygas (t.y. nesiskaido į
2 laipsnius ir pirminius Ferma skaičius). Tiesa, amžininkai į šią publikaciją dėmesio
neatkreipė ir praėjus 80 m. tapo gerai žinoma tarp matematikų. 2)
Ferdinandas Lindemanas (Carl Louis Ferdinand von Lindemann, 1852-1939) vokiečių
matematikas. Vystė įvairias matematikos sritis: Abelio funkcijų teoriją, projektyvinę, diferencialinę ir algebrinę
geometrijas, skaičių teoriją. Taip pat užsiėmė matematikos istorija ir sprektro analizės teorija.
Žinomiausias tapo įrodymu, kad p yra transcendentalus skaičius (t.y.,
nėra jokio polinomo šaknimi) tuo pačiu, kad neišsprendžiamas ir skritulio kvadratūros uždavinys. Daugelį metų
beviltiškai bandė įrodyti Didžiąją Ferma teoremą. Taip pat skaitykite: |
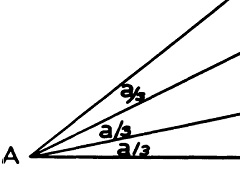 Kai kuriems kampams, pvz., 90o tai išsprendžiama lengvai.
Kai kuriems kampams, pvz., 90o tai išsprendžiama lengvai.